الوسم: القائم

الدائرة والمثلث القائم

كاتب المقالة بواسطة الشيخ مزياني
تاريخ المقالة 4 فبراير، 2022
لا توجد تعليقات على الدائرة والمثلث القائم

الدائرة والمثلث القائم

الدائرة والمثلث القئم

الملفات المرفقة

اسم الملف	نوع الملف	حجم الملف	التحميل	مرات التحميل
الــدائــرة و المثـلث القـائـم.rar‏		14.7 كيلوبايت		المشاهدات 48

الوسوم الدائرة, القائم, المثلث

الرياضيات للسنة الثالثة متوسط

الدائرة المحيطة بالمثلث القائم

كاتب المقالة بواسطة الشيخ مزياني
تاريخ المقالة 4 فبراير، 2022
لا توجد تعليقات على الدائرة المحيطة بالمثلث القائم

الدائرة المحيطة بالمثلث القائم

السلام عليكم ورحمة الله وبركاته
مع درس مهم جدا جدا جدا الا المثلث القائم وخواصه الجديدة التي سنعرفها من خلال هذا الدرس
وساقترح كتمهيد لهذا الدرس اختبار المكتسبات الموجود بالصفحة 152 من كتابة السنة الثالثة
والذي نصه يقول
1. ما ذا يمثل مركز الدائرة المحيطة بمثلث ؟
سمعتك تقول هو نقطة تقاطع المتوسطات هههههههه
لا يا حبيبي ؟ راجع معلوماتك
اسمع من هناك احد يقول انه نقطة تقاطع المنصفات هههههه
معليهش قاربت ولكن الاجابة غير صحيحة لان نقطة تقاطع المنصفات هي مركز لدائرة يحيط بها المثلث
اي المرسومة داخله والتي تلامس اضلاعه
اذن ما يمثل مركز الدائرة ؟ من هناك سمعت صوتا يقول انها نقطة تقاطع المحاور اممممممممم احسنت واجدت
فعلا هي نقطة تقاطع المحاور الثلاث لمثلث
ترى لماذا ؟
ساقترح عليك تمرينا يجيب على تساؤالي هذا اقلب صفحة الكتاب الى الخلف واقرأ التمرين 23 صفحة 151
ساجعل منك حلال لمشاكل الناس وفاهما لاهمية هذه النقطة
يقول نص التمرين
قام جدال ( مشادات لفظية فقط )بين أهل قرية أولاد قريب واهل قرية اولاد بعيد واهل قرية جبل الزيتون
حول موقع محطة القطار ( مبروك عليهم الكل وعلاش هذا الزعاف اما لا ؟)، اذ يريد سكان كل من القرى الثلاث ان تكون المحطة اقرب اليهم ( الطمع موش مليح والا سكانهم كبار؟ حتى شوفو مشيتهم )
كان الجدال حادا بين كبارالقرى ( الحمدولله لولاد الصغار مكانش )حينما تقدم بدر الدين ( انت او انت )طفل في الثالثة عشر قائلا : انا اعرف الحل !!!!!! (ازاقات عليه الليلة يقتلوا باباه بالضرب )لاني تعلمت في الهندسة كيف احدد موقعا يكون على نفس المسافة من القرى الثلاث ))
هل تستطيع انت ان تحدد هذا الموقع؟ اشرح
الحل
ما تقوليش منعرفوش
هذا هو التخطيط اللي لازم تديروا كما بدر الدين

الشرح
اكتفينا برسم محورين فقط لانهما يعينان موقع المحطة بدقة
المحور الاول هو محور : القطعة [قرية أ قريب وقرية أ بعيد]
المحور الثاني هو محور : القطعة [ قرية أ بعيد قرية جبل الزيتون ]
نقطة تقاطعهما هي موقع المحطة المطلوبة لانه ستبعد بنفس البعد عنهم جميعا (راجع خاصية نقط محور قطعة مستقيم )
نرجع الى الدرس
لنفكر ونحاول في النشاط 1 صفحة 153
يقول النشاط 1
1) abc قائم مثلث في النقطةa ، المستقيم (d) محور الضلع [ ac]

1-1 اثبت ان المستقيم(d) يقطع الوتر [bc] في منتصفه
– هل محور الضلع [bc] يشمل النقطة o ؟ علل جوابك
2- ما هو مركز الدائرة المحيطة بالمثلث abc ؟ علل جوابك
– ماذا يمثل الوتر [bc] بالنسبة لهذه الدائرة ؟

3- انقل واتمم الخاصية (( اذا كان مثلث قائما فإن…هذا المثلث هو … للدائرة المحيطة به ))
اضافة :

ماذا تمثل القطعة [oa] بالنسبة للوتر وكم يساوي طولها ؟

الحل

يمكن ان نثبت ان المستقيم (d) يقطع [bc] في منتصفهo
بعد ان نثبت ان (ab) // (d) وهذا باستعمال خاصية التوازي والتعامدالتي نصها (( المستقيمان العموديان على نفس المستقيم متوازيين ))
لدينا (ab) -|-(ac)
و(d)-|-(ac) نستنتج ان (d)//(ab)
في المثلث abc لدينا (d) يشمل منتصف [ac] ويوازي (ab)

اذن فهو يقطع [bc] في منتصفهo
2) محور[bc] يشمل النقطة o لان محور اي ضلع يمر بمنتصفه
اي ان o هي نقطة تقاطع محوري الضلعين [ac] و[bc] ومنه نستنتج ان oa=ob=oc اي ان o منتصف الوتر هي مركز الدائرة المحيطة بالمثلث القائم
– الوتر [bc]هو قطر للدائرة

نقل واتمام الخاصية (( اذا كان مثلث قائما فإن.. وتر.هذا المثلث هو .قطر.. للدائرة المحيطة به ))
القطعة [oa] هو متوسط متعلق بالوتر [bc]
oa = 1/2bc

من هذا النشاط يمكن ان نستخلص مايلي

** منتصف الوتر في المثلث القائم هو مركز الدائرة التي تحيط به **
** وتر المثلث القائم هو قطر للدائرة التي تحيط به **
** طول المتوسط المتعلق بالوتر في المثلث القائم = نصف طول هذا الوتر **

نلتقي ان شاء الله مع النشاط الثاني وتمرينات ان كتب الله

رد: الدائرة المحيطة بالمثلث القائم

مرسي مشكوررر افدتني كثيراااا

رد: الدائرة المحيطة بالمثلث القائم

شكرا على مجهودات المبذولة في توصيل شكرا

رد: الدائرة المحيطة بالمثلث القائم

merciiiiiiiiiiiiii

رد: الدائرة المحيطة بالمثلث القائم

احتاج الان بسرعة تمرين 27 صفحة 168 ارررررررررججججججججججججوووووووووككككككككككككككككممممم ممم انه واجب

رد: الدائرة المحيطة بالمثلث القائم

شكرا جزيلا اختي

الوسوم الدائرة, القائم, المثلث, المحيطة

الرياضيات للسنة الثالثة متوسط

المجسمات:: المكعب، متوازي المستطيلات، المنشور القائم، الأسطوانة الدائرية و الكرة .

كاتب المقالة بواسطة aksachli
تاريخ المقالة 4 فبراير، 2022
لا توجد تعليقات على المجسمات:: المكعب، متوازي المستطيلات، المنشور القائم، الأسطوانة الدائرية و الكرة .

المجسمات:: المكعب، متوازي المستطيلات، المنشور القائم، الأسطوانة الدائرية و الكرة…

المجسمات

المكعب

مجسم يتألف سطحه من 6 مربعات متطابقة تسمى أوجهه . وله 12 حرف و 8 رؤوس

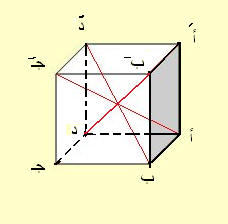
$الونشريس$

قانون حساب حجم المكعب = طول الحرف × طول الحرف × طول الحرف
= ( طول الحرف )3

مساحة المكعب = طول الحرف× طول الحرف ×6

متوازي المستطيلات
مجسم يتألف سطحه من 6 مستطيلات تسمى أوجهه . وله 12 حرف و 8 رؤوس .

قانون حساب حجم متوازي المستطيلات = ( طول القاعدة × عرض القاعدة ) × الارتفاع
= مساحة القاعدة × الارتفاع

المنشور القائم

مجسم له قاعدتان متوازيتان، تصل بينهما ثلاثة أسطح جانبية (جوانب).والقاعدتان مضلعان متطابقان في الشكل والمساحة. أما الأسطح الجانبية فهي متوازيات أضلاع.

وهناك أنواع متعددة من المناشير،وأبسطها ذو القاعدة المثلثة. وفي المنشور القائم الزاوية، تكون الأسطح الجانبية عمودية على القاعدتين
المساحه الجانبيه = محيط القاعده * الارتفاع
المساحه الكليه = المساحه الجانبيه +ضعف مساحه القاعده
الحجم = مساحه القاعده * الارتفاع

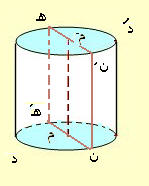
الأسطوانة الدائرية
هـى جسم له قـاعـدتـان مـتوازيتـان و متطابقـتان كـل منهـا عبـاره عن سطح دائره اما السطـح الجانبى هو سطـح منحن يسمى سطـح اسطوانى.

*بفرض ان نصف قطر القاعده (نق) ، الارتفاع (ع)

المساحه الجانبيه = 2 ط نق *ع
المساحه الكليه = 2 ط نق ( ع +نق )
الحجم = ط نق2 * ع

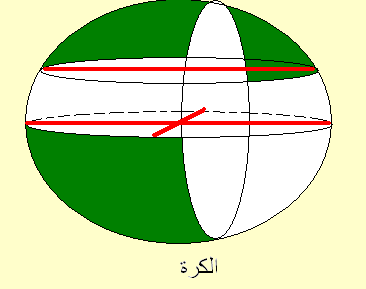
$الونشريس$

الكرة
هــى جسم يحده سطح مـنحن يسمى السطـح الكروى .

أو نقول
الكرة جسم محدد بسطح مقفل وجميع نقطه تقع على أبعاد متساوية من نقطة ثابتة.

تسمى النقطة الثابتة بمركز الكرة والبعد الثابت بنصف قطر الكرة (نق).

وتنشأ الكرة من دوران نصف دائرة دورة كاملة حول قطرها.

المقطع الحادث من قطع الكرة بمستوى يمر بمركزها هو دائرة نصف قطرها يساوي نصف قطر الكرة
، تسمى هذه الدائرة بالدائرة العظمى ويسمى المستوى بالمستوى المركزي أو القطري

إذا قطع كرة مستوى فالمستوى الحادث محيط دائرة صغرى ( المستوى لا يمر بالمركز)

$الونشريس$

مساحة الكره = 4 ***960; نق2
حجم الكره =4/3 ***960; نق3

المخروط
السطح المخروطي يتولد من حركة مستقيم مار بنقطة ثابتة وقاطع محنى مستوى معلوم. فالمنحنى هو محيط قاعدة المخروط والمستقيم يسمى راسم السطح المخروطي ويسمى في أ وضع راسم وإن كان المنحنى دائرة قيل مخروط دائري وكذلك المخروط حالة خاصة من الهرم قاعدته دائرة وإذا مر الارتفاع بمركز القاعدة قيل مخروط دائري قائم، ومقطع المخروط الناشئ من قطعه بمستوى يمر برأسه والقاعدة هو مثلث متساوي الساقين وإذا قطع المخروط بمستوى يوازي القاعدة نشأ المخروط الدائري المتوازي القاعدتين،

كما ينشأ المخروط الناقص الدائري القائم من دوران شبه منحرف قائم حول ارتفاعه دورة كاملة.

كما يتولد المخروط الدائري القائم من دوران مثلث قائم حوا أحد ضلعي القائمة.

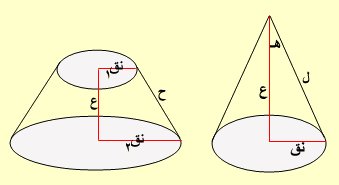
$الونشريس$

* حجم أي مخروط V هو ثلث جداء مساحة القاعدة b بالارتفاع h , أي:

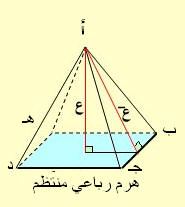
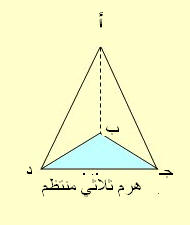
$الونشريس$

الهرم

إذا علم مضلع مستو ونقطة خارجة ووصلت برؤوس المضلع تكونت عدة مثلثات قواعدها أضلاع المضلع والجسم الذي تحدده سطوح هذه المثلثات وسطح المضلع يسمى هرم.

قاعدة الهرم هي ذلك المضلع والرأس المشترك للمثلثات هو رأس الهرم والمثلثات هي أوجه الهرم الجانبية والعمود النازل من رأس الهرم على قاعدته هو ارتفاع الهرم ويسمى الهرم حسب عدد أضلاع قاعدته فإن كانت مثلث قيل هرم ثلاثي ويسمى الهرم قائم إذا كان موقع العمود من الرأس على القاعدة وهي مضلع منتظم هو مركز القاعدة (المضلع المنتظم ما كانت أضلاعه وزواياه متساوية كالمثلث المتساوي الأضلاع).

إذا قطع الهرم بمستوى يوازي قاعدته نشأ هرم ناقص متوازي القاعدتين النسبة بين مساحتي القاعدتين كالنسبة بين مربعي بعديهما عن رأس الهرم.

$الونشريس$
$الونشريس$

حجم الهرم = 1/3 * مساحة القاعدة * الارتفاع

رد: المجسمات:: المكعب، متوازي المستطيلات، المنشور القائم، الأسطوانة الدائرية و الكرة.

100000 شكرا لك

وجزاك الله كل خير