ارجوكم اريد حل لتمرين حول النسب المثلثيه
a bc مثلث قائم في a
ارسم منصف الزاوية b اذ يقطع ac في g
احسب بالتدوير 0.01 الطول ag
هناك نقص في معلومات التمرين
منصف زاوية ما: هو منصف للضلع المقابل لهذه الزاوية
إذن مباشرة إذا علمنا طول [ac] نجد مباشرة طول الضلع [ag] ألا و هو النصف (ag = 1/2 ac)
شكرا جزيلا على هذا الجهد


نابغة جزائري يكتشف نظرية جديدة في الرياضيات
تمكن التلميذ النابغة جمال الدين بنعيشة من سطيف من اكتشاف نظرية جديدة في حساب مساحة المثلث تعتبر أفضل بديل لنظرية هيرون المعمول بها منذ قرون.
هذا الاكتشاف الذي قد يكون له شأن عظيم في المستقبل جاء من تلميذ يدرس في السنة الثانية ثانوي والذي قال للشروق اليومي أن الصيغة المستعملة حاليا والتي اكتشفها العالم هيرون الاسكندري في العصر البطلمي بعد العصر الفرعوني وهي مصرية الأصل عيبها الوحيد أنها تأخذ وقتا طويلا عندما يكون المثلث المراد حساب مساحته له أطوال تحـوي جذورا تربيعية ويكون حينئذ احتمال الوقوع في الخطأ كبير، خاصة في عمليات النشر والتبسيط. ولذلك يقول جمال الدين اكتشفت صيغة جديدة تحل هذا المشكل ويمكن حساب المساحة بسهولة وبدون عناء مع اجتناب عمليات النشر الطويلة. وقد تم طرح هذه النظرية على أساتذة جامعيين واعترفوا بالصيغة الجديدة التي استعملها جمال الدين الذي يؤكد بأنه يملك البرهان الكامل لهذه النظرية ومتيقن بأنه لم يتوصل اليه اي باحث من قبل. للإشارة فإن جمال الدين البالغ من العمر 17 سنة، يدرس في السنة الثانية، ثانوي تحصل على علامة 20 في مادة الرياضيات خلال الفصلين الأول والثاني وعلامة 17 في الفيزياء، وقد عرف بذكائه الثاقب واعتاد على تصحيح أخطاء الأساتذة دون إحراجهم. ويقول أن والدته (الطبيبة) هي التي حفزته لاكتشاف هذه النظرية الجديدة التي يمكن أن تدرس في الجامعات. وأما عن طموحه، فيقول بأنه يريد أن يصبح طبيبا جراحا لإنقاذ حياة المرضى.. وفي الوقت الحالي يدعو كل الأساتذة إلى الاطلاع على نظريته ويقول بأنه ليس سعيدا من أجل نفسه بقدر ما هو سعيد من أجل بلده الجزائر .
ما شاء الله
مااااا شاء الله ربي يحفظه لوالديه
ماشاء الله رب يحفظو بصح وين راها النظرية
ماشاء الله ربي يحفضواا
ماشاء الله لكن اين هي النظرية اريد ان استفيد منها *
ما شاء الله طفل ذكي بمعنى الكلمة حفضه الله
ابارك لوالديه هذه النعمة المروعة التي انعمهما بها
ولكن اين هاته النضرية فقد دفعني الفضول للتعرف عليها
تسلمي اختي على زهرة مجهودك البراااق
merci beaucoup
ماشاء الله
الحمد لله اننا بدءنا في التقدم شيئا فشيئا
الخبر يجعلني أحس بالافتخار بابناء وطني
و الفضول يدفعني للاطلاع على مضمون
النظرية الجديدة.
الله اكبر ولكن انا اريد النظريةةةةةةةةةةةةةةةةةةةةةةةةةة جبتوا قشور بلا زريعة اين هي النظرية المتكشفة ااااااااااااااااااااااا
المثلث التعليمي

المعلم و المادة التعليمية
المعلم و التلميذ
تعريف المثلث التعليمي:
هو المثلث الذي يسمح بتبيان العلاقة بين المعلم و التلميذ و المادة التعليمية، وهو عبارة عن تشكيلة مكونة من ثلاث علاقات هي:
– علاقة بين المعلم و التلميذ ( يركز على النشاط التعليمي الموكل للمعلم).
– علاقة بين المعلم و العلم (الذي يجسد مبادراته في عملية تحضير وهيكلة الدرس من طرف المعلم).
– علاقة بين العلم والتلميذ( يركز على عملية التعلم عند التلميذ).
Ý- العلاقة بين التلميذ و العلم:
نشأت فكرة العلاقة بين التلميذ والعلم بناءا على فشل التربية التقليدية التي تجعل من المتعلم فردا محايدا في العملية التربوية و كرفض لذلك جاءت التعليمية لكي لا تعتبر عقول التلاميذ علبا فارغة ينبغي حشوها بالمعرفة بل هم أفراد فعالون و يشاركون في بناء تعلمهم بالاعتماد على معارفهم السابقة أو بناءا على ما اكتسبوه خارج المدرسة.
ȝ- العلاقة بين المعلم و العلم:
يحدد البرنامج الدراسي وحجم العلم اللازم تدريسه يقوم المعلم بإدماج هذه المعرفة عن طريقته، يتخذها كنقطة انطلاق إلا أنه لا يعيدها كما هي بل يخرجها من إطارها الأصلي ليضع لها إطار جديد و ذلك وفق مستوى تلاميذه ووفق اختياراته المنهجية و أهدافه الخاصة.
ج- العلاقة بين المعلم و التلميذ:
نسمي هذه العلاقة بالعقد التعليمي وهو العقد الذي يبرم بين المعلم و تلاميذه أي القوانين الإدارية و كذا ما نص عليه التشريع المدرسي هي التي تحدد العلاقة بين التلاميذ و المعلم ( القانون الداخلي للمدرسة)، إذن العقد التعليمي تمثله مجموعة هذه القوانين التربوية والأفعال السلوكية في المدارس والمؤسسات الموجودة بها هذا العقد وهدفه هو وضع آليات التعليم أو التقييم ونزع محل الصعوبات التي تعيق من عملية التعليم ، مثل التأخير.
منقول للفائدة


سلام أيها الأحبة أنا عضو جديد أخوكم لويفي خالد من متوسطة "بوروبة الجديدة" من الجزائر العاصمة
أريد المساهمة بهذه الأعمال المتواضعة إثراء هذا الموقع المحترم و هاهي الأعمال
| اسم الملف | نوع الملف | حجم الملف | التحميل | مرات التحميل |
| العلاقات المثلثية في المثلث القائم.rar | |
680.1 كيلوبايت |  |
المشاهدات 179 |
| اسم الملف | نوع الملف | حجم الملف | التحميل | مرات التحميل |
| تظرية طاليس.rar | |
244.7 كيلوبايت |  |
المشاهدات 127 |
شكرا انجاز رائع
| اسم الملف | نوع الملف | حجم الملف | التحميل | مرات التحميل |
| العلاقات المثلثية في المثلث القائم.rar | |
680.1 كيلوبايت |  |
المشاهدات 179 |
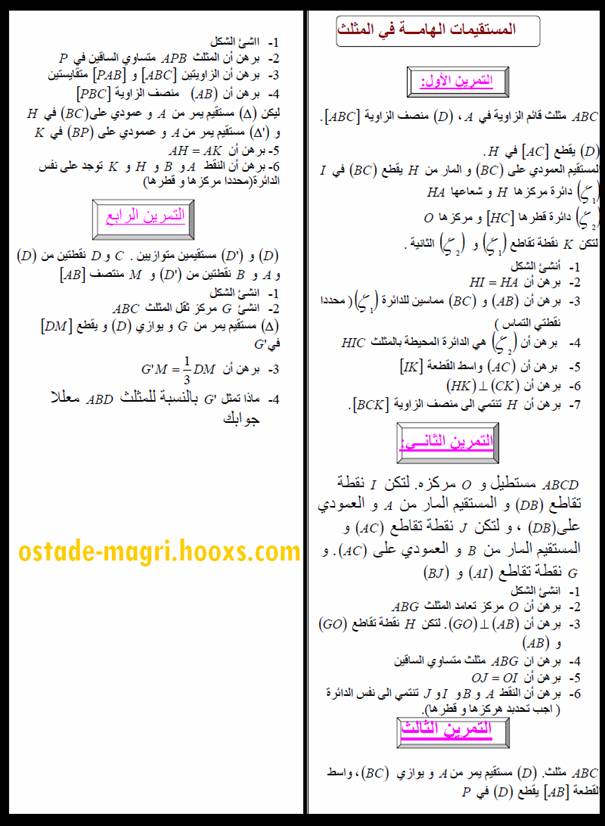
خواص المستقيمات في المثلث

خواص المستقيمات في المثلث
المستوى : ثالث متوسط http://www.up-00.com/dldWK807590.doc.html
|
رد: خواص المستقيمات في المثلث
شكرا جزيلا أختي بارك الله فيك درس سهل
|
رد: خواص المستقيمات في المثلث
ميـــــــــــــــــــــــــرســـــــــــــــــي…
|
رد: خواص المستقيمات في المثلث
تسلما على مروركما الطيب
|
رد: خواص المستقيمات في المثلث
شكراااااااااااااااااااااااااا
|
رد: خواص المستقيمات في المثلث
هل هذا هو محتوى الدرس ( b>Warning</b>: [obfuscated](http://store1.up-00.com/Jun10/WK807590.doc) [<a href=’function.[obfuscated]’>function.[obfuscated]</a>]: failed to open stream: HTTP request failed! HTTP/1.1 404 Not Found </body>
| المثلث المتقايس الأضلاع ـ المربع ـ السداسي المنتظم

الكفاءة القاعدية : إنشاء مضلعات منتظمة المراحل
مؤشرات الكفاءة أنشطة التعلــــــــــــــــم
التقويــــــم نشاط وضعية الإنطلاق تمثيل المعرفة التفريق بين المضلعات المنتظمة و الغير منتظمة صياغة المفاهيم و المعارف المكتسبة نشاط 6 ص 228 : كتابة معرفة 4 ص 232 و الخاصيات 1 ، 2 ، 3 ص 233 ملاحظة : متى نقول عن مضلع أنه مضلع منتظم ماذا نقول عن الزوايا المركزية في المضلع المنتظم ؟ ـ ماهي الطريقة المتبعة لإنشاء كلا من مثلث متقايس الأضلاع ـ
ـ 43 ـ
|
رد: المثلث المتقايس الأضلاع ـ المربع ـ السداسي المنتظم
شكرا لكي اختي على الموضوع بارك الله فيك
|
رد: المثلث المتقايس الأضلاع ـ المربع ـ السداسي المنتظم
رائع شكرا.الي القاء
| الدائرة والمثلث القائم

الدائرة والمثلث القئم |