انشاء سداسي منتظم
انشاء معين
انشاء معين باستعمال خاصية قطريه
انشاء مستطيل بمعلومية طول احد اقطاره
انشاء مستطيل بمعلومية طول ضلعين متتالين من اضلاعه
انشاء خماسي منتظم
يتبع…
انشاء متوازيان بالمدور والمسطرة
انشاء منصق زاوية يالمدور والمسطرة
انشاء ثماني منتظم
يلي
…..دوختني يا اخي ……..
……….شكراااااا جزيلا ………….
..*وحيدة كالقمر*..
.
اقتباس 
| ….دوختني يا اخي …….. ……….شكراااااا جزيلا …………. |
اتمنى انهم عجبوك
الف شكرا على الرد والتعقيب
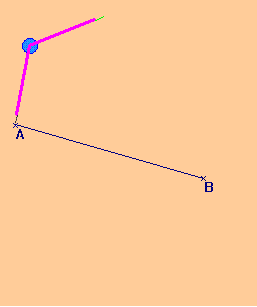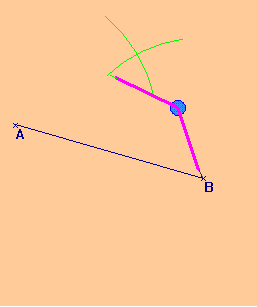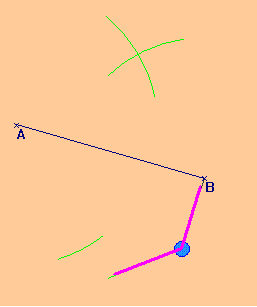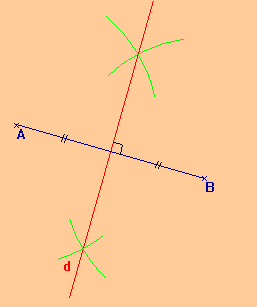
انشاء محور قطعة مستقيم ( مستقيمان عموديان)
انشاء مثلث مساخته تساوي مساحة مربع
خواص متوازي اضلاع
جزاك الله خير
صورة لانشاء العدد الذهبي
رابط الحفظ
http://www.maths.ac-aix-marseille.fr…mediatrice.swf
انشاء المستقيم المواز لاخر والذي يمر من نقطة لا تنتمي اليه بالمسطرة والكوس
انشاء نظير شكل بالنسبة الى مستقيم
انشاء مستقيم عمودي على اخر ويشمل نقطة لا تنتمي اليه بالمسطرة والكوس
انشاء مستطيل بالكوس والمسطرة
الان ناتي الى انشاءات بالمدور فقط لبعض الزوايا المنشأة لكن الصور غير متحركة
1) زاوية قياسها 60°
زاوية قائمة
زاوية 45°
زاوية 30°
زاوية 15°
كما تلاحظون يمكن انشاء زاوية قيسها 7.5° وهذا بتنصيف الزاوية 15°
اذا احتجتم اي شرح سافعل
حافظوا على فتحة المدور في الزوايا60° و 90°
الان مع شكل يظهر خاصية المماس لدائرة و نوع المثلث الذي احد اضلاعه قطر لدائرة
استخدام المنقلة لقياس زاوية
وتربيع مستطيل بنقصان هههههه
مجموع اقياس الزاويا الخارجية لمضلع =؟؟؟؟؟؟
شوفو الصور
في سداسي منتظم
في خماسي منتظم
في سباعي منتظم
في ثماني منتظم
في تساعي منتظم
في عشاري منتظم
الان يمكن ان نصل الى قاعدة نصها ان مجموع الزوايا الخارجية لمضلع
= قيس الزاوية الخارجيةله في عدد الاضلاع = 360°
الشكل الناتج من منتصفات الاضلاع هو متوازي اضلاع
منحنى دائرة يتغير نصف قطرها
واختم بصور رااااااائعة لجمال الاشكال الهندسية
احفظوا الصور قبل ان تطير هههههه
الاثني عشر
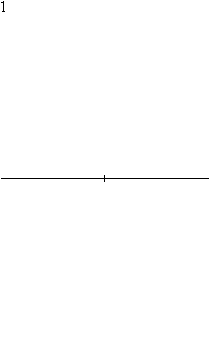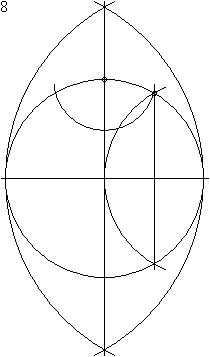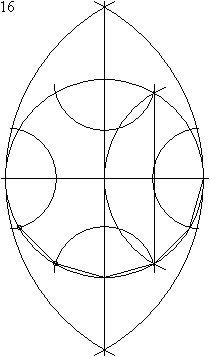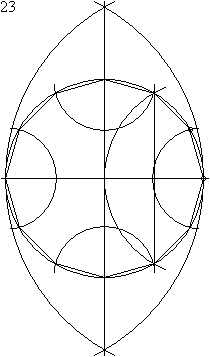
ذو سبعة عشر ضلعا معقد وغير واضح تماما
مثلث متساوي الاضلاع
ثماني منتظم طريقة اعقد
صور رائعة ومفيدة احسنت الاختيار…………..
الف شكر حبدا لواتحفتنا باشكال هندسية كمتوازي المستطيلات القائم و المكعب في الفضاء ولك مني الف تحية
تم دمج موضوعي الاخر مع هذا الموضوع لانهما يصبان في نفس الجهة
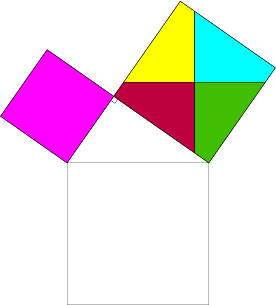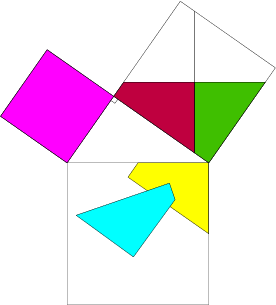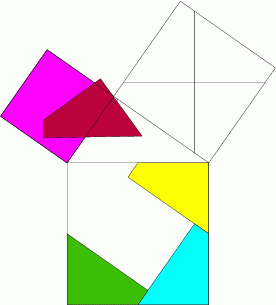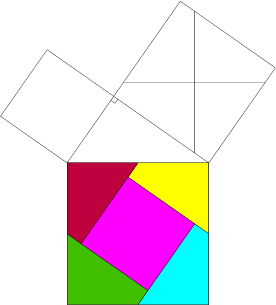
برهان نظرية فيثاغورث
انشاء (رسم) سداسي منتظم
قطع مخروط بمستو
لا ادر بما اعلق على هذه الصور
المكعب
تعلم الكسور الممتع
مكونات ذرات بعض العناصر الكيميائية
لاصحاب الفيزياء
احجية صينية بالصورة
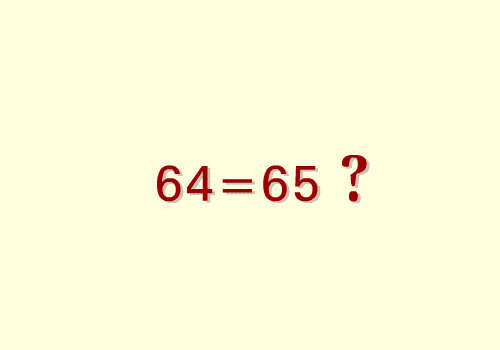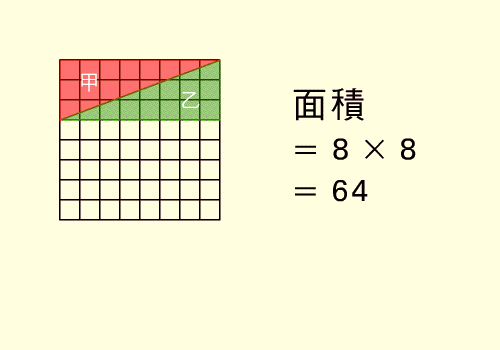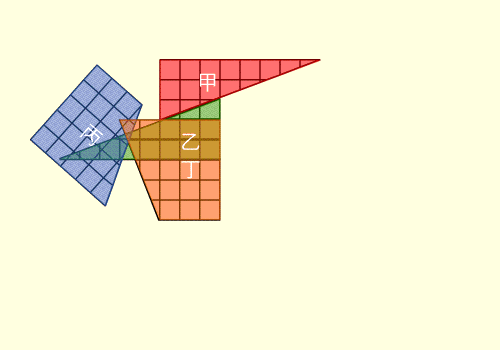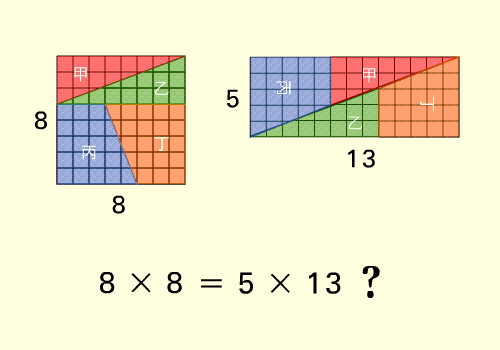
طريقة ايجاد القاسم المشترك الاكبر للعدين1071 ،462
شرحها بالانجليزية
Animation of the algorithm. The initial green rectangle has dimensions a = 1071 and b = 462. Square 462×462 tiles (yellow) are added until a green 462×147 rectangle remains. This is tiled with square 147×147 tiles (blue) until a 21×147 rectangle remains. This third rectangle is tiled with 21×21 square tiles (red), leaving no remainder. Thus, 21 is the greatest common divisor of 1071 and 462.
